Lineare Regression u. nicht-lineare Funktionen

Mit LINREG  steht ihnen eine nützliche Anwendung der Methode der kleinsten Quadrate zur Verfügung -  die Beschreibung einer Menge experimenteller Daten durch eine Kurve oder eine theoretische Formel, um eine lineare oder nicht-lineare  Beziehung zu erhalten,  die am besten auf die Daten passt - bei möglichst kleinem Fehler.

LinReg  besteht aus den Programmteilen:

• ✔
  lineare Regression
• ✔
  nicht lineare Funktionen- Geraden – Gleichungen

Anwendungsbereiche:

Auswertung von Messwerten und Erfassung der  Messwert-CharakteristikKalibrierung von Messsystemen durch lineare Regression Erkennen von Zusammenhängen innerhalb einer UntersuchungsreiheDarstellung von Abläufen mit linearem oder nicht-linearem Bezug

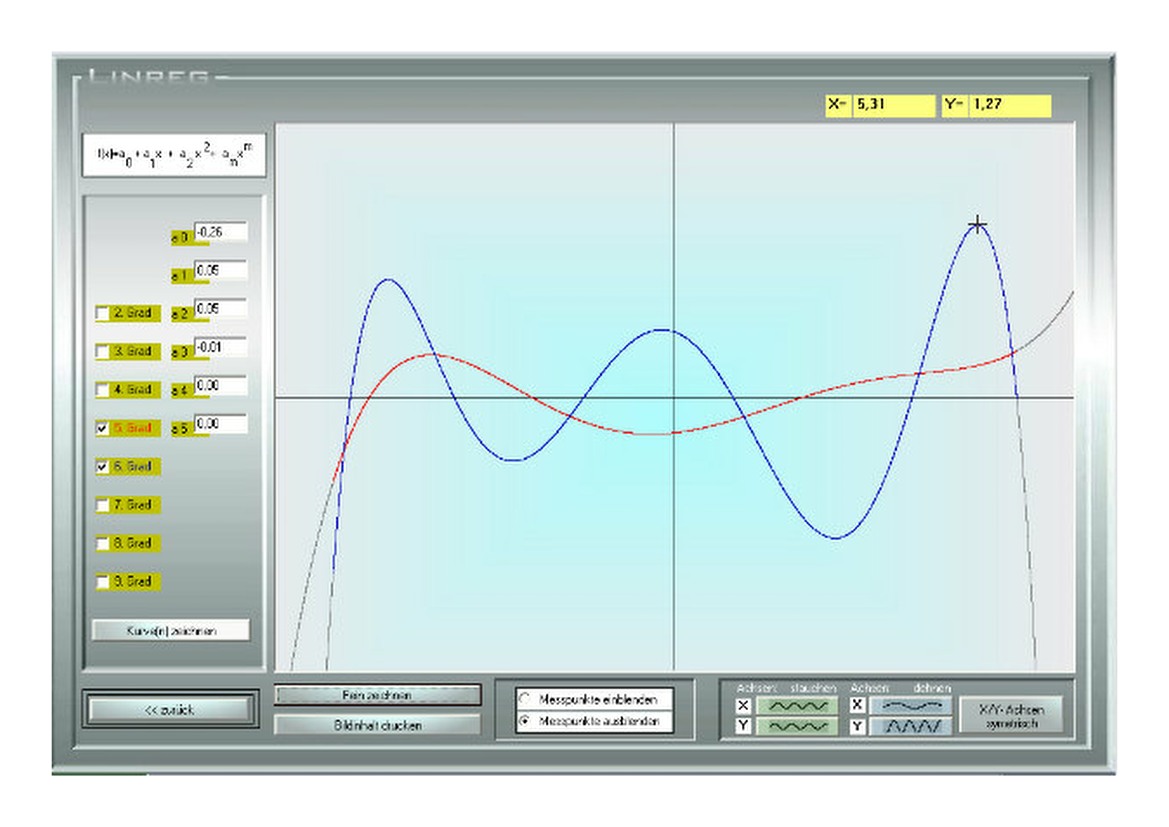
Errechnung einer mathematischen Gleichung nach Y = ax + b oder wahlweise für einen nicht-linearen  Zusammenhang bis zum 9. Polynom nach :            Y= a0 + a1x +a2x2 +a3x3 ..... + amxm

Erstellung einer Berechnungsformel aus einer Werte-Tabelle Beispiele:  

• ✔
  Erstellung von Kennlinien für Pumpen
• ✔
  Eichkurven für Photometrie - Polarimetrie - AAS - etc.
• ✔
  Erstellung von Leistungskurven für Maschinen, grafische Darstellung der Kurven mit manueller Änderungsmöglichkeit der Koeffizienten

Erstellung eines mathematischen Zusammenhangs aus Grafik- Vorlagen zur Übernahmein Rechenprogramme

lineare Regression Berechnungen:

• ✔
  mathematischer Zusammenhang der Wertepaare als Funktion von x nach: f(x)= ax +b für Geraden mit und ohne Achsenabschnitt (b=0) Möglichkeit der Berechnung mit zwingen durch 0/0

• ✔
  Fehler für Steigung und Achsenabschnitt.
• ✔
  Fehler für jeden einzelnen Messwert in % und absolut.-
• ✔
  Korrelations-Koeffizienten.

Grafische Darstellung der berechneten Funktion am Bildschirm - bei variablerAchs-GeometrieZur Optimierung der Berechnung können zusätzlich Wertepaare angehängt, gelöscht oder geändert werden.

nicht-lineare Funktio​​nen

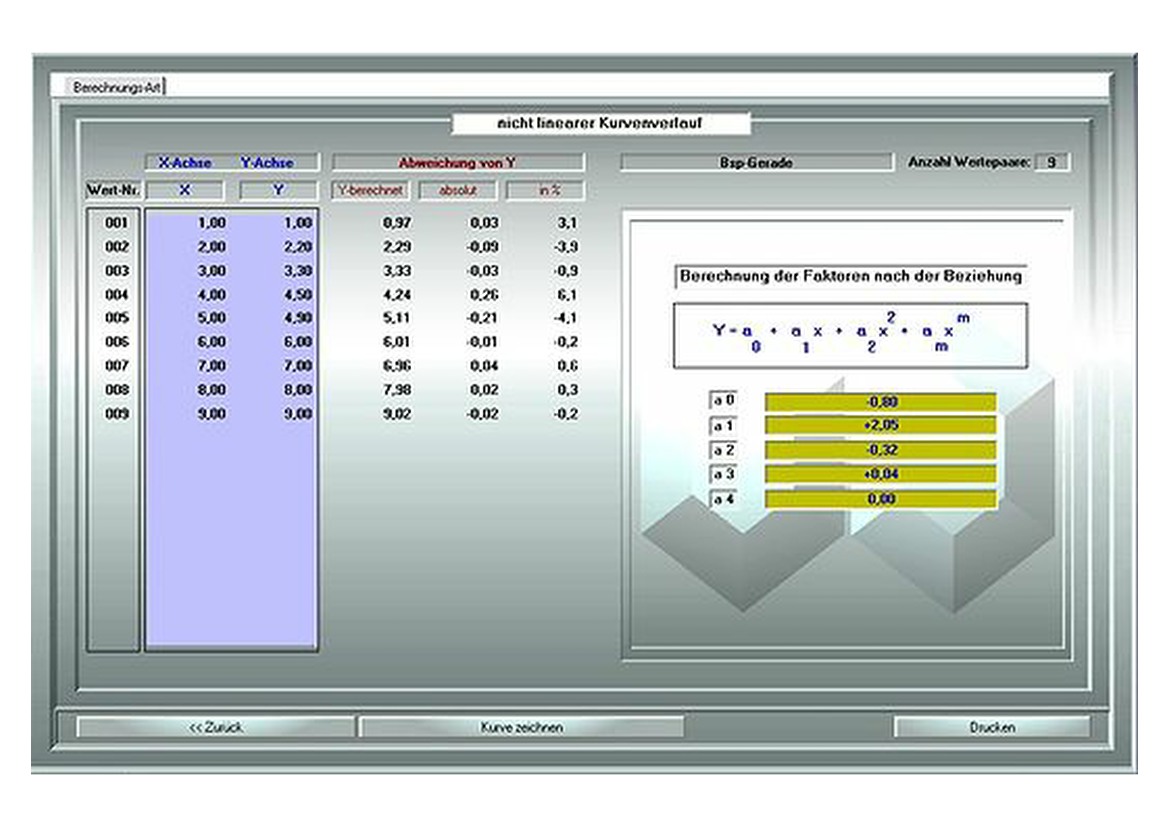
Zur Darstellung von Funktionen oder technischen Abläufen mit mathematischen Verknüpfungen bei nicht linearem Kurvenverlauf.     
Erstellung einer Formel aus einer Werte-Tabelle mit nicht-linearem Verlauf
Erfassung von Abläufen mit  nicht-linearem Charakter

Anwendungsbereiche:

• ✔
  Erstellung von Kennlinien oder Absorptionskurven
• ✔
  Leistungskurven für Maschinen
• ✔
  Umformen von Berechnungsformeln in eine Funktion n. Grades

Aus einer Reihe von Messwerten wird eine mathematische Funktion bis zum 9. Polynom berechnet. 
Grafische Darstellung der berechneten Funktion am Bildschirm 

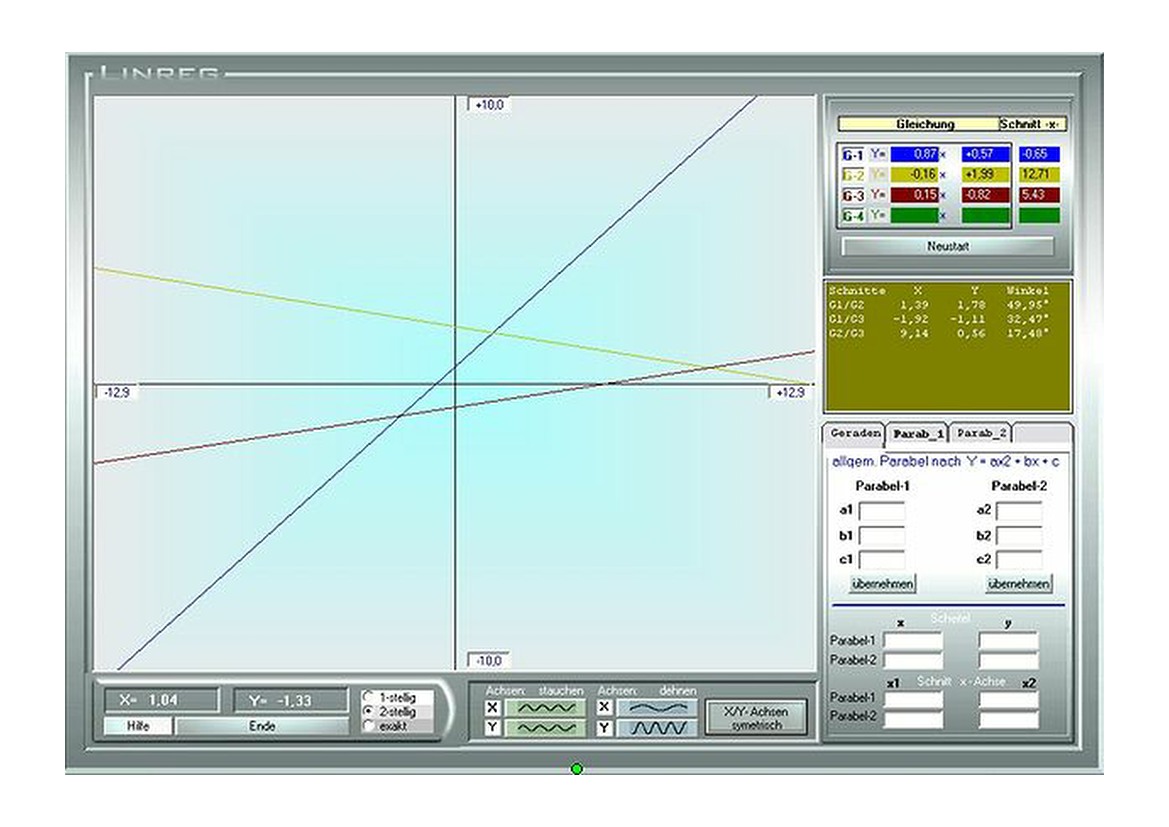
Geraden-Gleichungen

manuelles zeichnen von Geraden im Koordinatensystem
Vorgabe von Steigung + Achsenabschnitt oder von 2 Punkten 
Berechnung von Schnittpunkt, Schnittwinkel, Achsendurchbruch
Darstellung von Parabeln mit   X/Y- Symetrie  sowie der Form Y = ax² + bx + c

Features

Eingabe und Berechnung mit wählbarer Stellenzahl
Archivierung der Kurven + Berechnungen mit Änderungs- u. Ergänzungs- Möglichkeit
Regressions-Berechnung mit Verlauf zwingen durch 0/0
Anzeige des Streubereichs einer berechneten Kurve
Ein/Ausblenden der Messpunkte in einer grafischen Darstellung
individuelle Farb-Einstellung zur grafischen Darstellung
Achsen können gestreckt oder gestaucht werden (Zoomen)
Darstellung von bis zu 4 Kurven in einem Bild